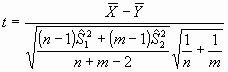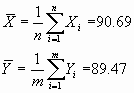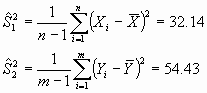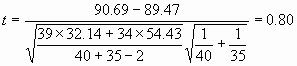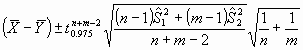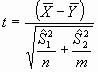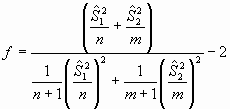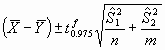Pruebas pareadas para variables cuantitativas
Si estamos comparando un resultado cuantitativo en dos grupos de datos,
a partir de muestras extraídas de forma aleatoria de una
población normal, siendo nA el tamaño de la
primera muestra y nB el de la segunda, la cantidad:
(donde

son las medias muestrales,

las
correspondientes medias poblacionales,
s
la desviación típica muestral conjunta), se distribuye como
una
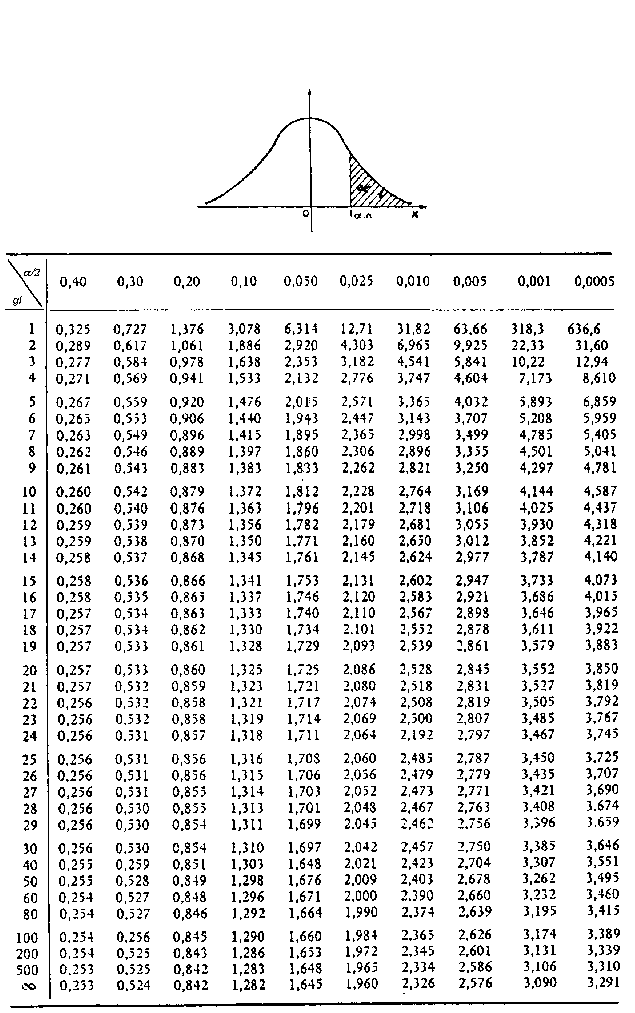
t de Student con
nA+nB-2
grados de libertad, proporcionándonos una referencia probabilística
con la que juzgar si el valor observado de diferencia de medias nos
permite mantener la hipótesis planteada, que será
habitualmente la hipótesis de igualdad de las medias (por ejemplo
igualdad de efecto de los tratamientos), o lo que es lo mismo nos permite
verificar si es razonable admitir que

a la luz de los datos obtenidos en nuestro experimento.
Veamos un pequeño ejemplo. Se efectuó un estudio para
comparar dos tratamientos en cuanto a la mejoría en la salud
percibida, determinada mediante un cuestionario de calidad de vida en
pacientes hipertensos. Se asignaron 10 pacientes de forma aleatoria a cada
uno de los grupos de tratamiento, obteniéndose los siguientes
resultados:
| Trat. A |
5.2 |
0.2 |
2.9 |
6.3 |
2.7 |
-1.4 |
1.5 |
2.8 |
0.8 |
5.3 |
| Trat. B |
6.0 |
0.8 |
3.2 |
6.2 |
3.8 |
-1.6 |
1.8 |
3.3 |
1.3 |
5.6 |
Si calculamos el valor de t según la fórmula
anterior obtenemos:
Tabla 2
| Dif.medias |
0.41 |
| Err.est.dif. |
1.11 |
| t Student |
0.37 |
| gl |
18 |
| P |
0.7165 |
| Intervalo 95% para la dif. de medias |
-1.93 a 2.75 |
|
Tabla 3
|
Trat. A |
Trat. B |
| Media |
2,63 |
3,04 |
| Desv.Típ. |
2,45 |
2,52 |
|
|
Figura 1
|
De acuerdo con esos resultados, al ser la probabilidad obtenida
alta, vemos que no hay razones para rechazar la hipótesis de
que no existe diferencia entre los grupos (P= 0.7165), aceptamos que
las medias son iguales, lo que podemos también comprobar de
forma gráfica, si representamos cada serie de valores en dos
posiciones del eje X, obteniendo un gráfico como el
representado en la figura 1.
Ahora bien, sabemos que dos variables que influyen en los resultados
de los cuestionarios de calidad de vida percibida son la edad y el
sexo de los pacientes. Al asignar de forma aleatoria los pacientes a
cada grupo de tratamiento esperamos que las variables que puedan
influir en el resultado, diferentes del propio tratamiento asignado,
se distribuyan en ambos grupos de forma parecida; pero cuando de
antemano conocemos que algunas variables sí influyen en el parámetro
objeto de estudio, podemos controlarlas en el diseño para
evitar que puedan afectar al resultado, sobre todo cuando vamos a
trabajar con una muestra pequeña.
Así en nuestro ejemplo podemos dividir los pacientes dentro
de cada sexo en varios grupos de edad y buscar parejas de pacientes
con el mismo sexo y con edades similares. Dentro de cada pareja,
seleccionada con ese criterio (igual sexo y edad similar), asignamos
de forma aleatoria cada uno de los tratamientos.
Esto es lo que precisamente habíamos hecho en el estudio de
la tabla 1: habíamos dividido la edad en
5 categorías y seleccionado 5 parejas de hombres y 5 de mujeres
en cada grupo de edad. Dentro de cada par hemos asignado de forma
aleatoria el tratamiento A o el B a cada uno de sus elementos. |
En este caso hemos "diseñado" un estudio, en el que
mediante el emparejamiento estamos controlando (o bloqueando) la
influencia de las variables edad y sexo.
Ahora en el análisis estadístico de los datos, para
tener en cuenta el diseño, hay que comparar cada pareja de
valores entre sí. |
Pero antes de hacer un análisis estadístico vamos a
representar gráficamente el nuevo planteamiento.
Si calculamos las diferencias entre el valor del elemento B y el
elemento A y las representamos gráficamente obtenemos la figura
2, donde hemos dibujado una línea horizontal en el valor 0, que
corresponde a la igualdad entre los tratamientos. |
Figura 2
|
| Vemos que el panorama cambia radicalmente con respecto a la
figura 1, ya que ahora la mayor parte de los
puntos están por encima de esa línea de igualdad de
efecto, reflejando una mayor puntuación por término
medio en el tratamiento B que en el A dentro de las parejas. |
En la siguiente tabla vemos los resultados del análisis estadístico,
muy diferentes de los obtenidos en la tabla 1 en la
que no se tenía en cuenta el tipo de diseño:
Tabla 4
| Dif. B - A |
Resultado |
| Media |
0,410 |
| Desv.Típ. |
0,387 |
| Tamaño |
10 |
| Err.est.dif. |
0,122 |
| t Student |
3,349 |
| gl |
9 |
| P |
0,0085 |
| Int. conf. 95% para la media |
0,133 a 0,687 |
Ahora hemos calculado la media de las diferencias d, y su
desviación típica sd en las n
parejas. El error estándar de la media de las diferencias es:
Por lo que el valor de t será ahora
que en la hipótesis de igualdad -media de las diferencias igual a
cero-, se distribuye como una t de Student con n-1 grados de
libertad.
Aunque perdemos grados de libertad, siendo por ese lado la prueba menos
potente, sin embargo al disminuir la variabilidad se aumenta la eficiencia
de la prueba. No siempre será tan dramática la diferencia
entre ambos planteamientos, ya que en este caso se trata de datos
preparados y en la realidad las cosas no suelen salir tan redondas.
Cuando efectivamente influye en el resultado la variable que nos ha
llevado a decidir utilizar un diseño pareado, las medidas dentro de
cada pareja estarán correlacionadas, por lo que siempre podemos
comprobar a posteriori si esto es así, calculando el coeficiente de
correlación, que debiera ser positivo y de cierta entidad.
El concepto de prueba pareada se puede extender a comparaciones de más
de dos grupos y hablaremos entonces de bloques de m
elementos (tantos elementos por bloque como grupos o tratamientos), siendo
por tanto una pareja un caso particular de bloque de 2 elementos.
Hablaremos de este tipo de diseños más adelante, cuando
dediquemos algún artículo al análisis de la
varianza, que es la prueba que se utiliza para comparar más de
dos grupos. En estas técnicas de formación de bloques el
investigador deja de ser un mero observador, para pasar a "diseñar"
el estudio o experimento, y es una metodología de gran utilidad en
muchos tipos de trabajos de investigación en diversas áreas,
desde la agricultura donde se inició, a la medicina, biología,
e ingeniería. El fundamento en el que se basan es en suponer que el
bloque es más homogéneo que el conjunto, por lo que
restringiendo las comparaciones entre tratamientos al interior de los
bloques se espera obtener una mayor precisión.
Hay que destacar que no siempre el diseño pareado es el más
efectivo, ya que como se apuntó anteriormente hay una disminución
en los grados de libertad que debe ser compensada con la reducción
de varianza para que la prueba resulte más efectiva. Hay muchas
situaciones en las que las observaciones "próximas" están
relacionadas negativamente, de tal manera que las comparaciones entre
parejas son entonces menos parecidas que otras comparaciones.
En los estudios clínicos el emparejamiento se utiliza
habitualmente más que por razones de eficiencia para "aumentar"
la validez de las inferencias obtenidas, mediante el control de posibles
variables confusoras. Por ello se desaconseja, en el criterio para
emparejar, la utilización de variables sobre las que no estemos
seguros de su influencia en el resultado de interés.
Pruebas pareadas para variables cualitativas
El concepto de diseño pareado se puede aplicar también al
análisis de datos cuyo resultado es una categoría. Veamos la
situación más sencilla, para el caso de que la variable
cualitativa sea dicotómica o binaria, con sólo dos posibles
repuestas. Este planteamiento es habitual en algunos estudios
de casos-controles, en los que cada caso se empareja con un
control de acuerdo con un criterio determinado, y en el que se trata de
valorar la frecuencia de la presencia de un factor de riesgo. Podemos
representar los resultados en una tabla de la siguiente forma:
|
|
Controles |
|
|
|
Factor presente |
Factor ausente |
|
| Casos |
Factor presente |
a |
b |
a+b |
| Factor ausente |
c |
d |
c+d |
|
|
a+c |
b+d |
n |
donde en cada celda se refleja el número de parejas; así
a es el número de parejas en las que el factor de riesgo
está presente tanto en el caso como en el control, y d es
el número de parejas en las que ni en el caso ni el control se da
el factor de riesgo. Es evidente que en esas dos celdas hay concordancia
entre lo observado en el caso y lo observado en el control, dentro de la
pareja, y que por tanto no afectarán al resultado en cuanto a
diferencias entre casos y controles, siendo sólo los pares
discrepantes b, c los que aportan información en ese
sentido.
La proporción de controles que presentan el factor de riesgo es
y la proporción de casos con el factor de riesgo
La diferencia de proporciones en cuanto a presencia del factor de riesgo
entre casos y controles es:
donde como ya anticipábamos las cantidades a y d
no intervienen. El error estándar de esa diferencia viene dado por:
El cuadrado del cociente entre la diferencia y su error estándar,
se distribuye bajo la hipótesis de igualdad como una chi² con
1 grado de libertad, y el contraste se conoce como prueba de McNemar:
Si se aplica la corrección de continuidad (recomendable sobre
todo si el tamaño de muestra es pequeño o hay celdas con
frecuencias pequeñas), la fórmula anterior se modifica
ligeramente:
Para estimar el
odds ratio en este tipo de
diseño se utiliza la fórmula:
donde de nuevo solo intervienen los pares con desacuerdo.
El error estándar de este odds ratio se calcula como
En una primera impresión puede sorprendernos la fórmula
para el cálculo del odds ratio, pero su obtención es
sencilla si pensamos que en realidad cada pareja es un estrato con 2
elementos, y que no debemos combinar las tablas obtenidas en cada estrato
juntándolas sin más. Si aplicamos para el cálculo del
odds ratio combinado el método habitual conocido como de Mantel-Haenszel
obtendremos la fórmula anterior.


 T = 7 / 4 = 1.75
T = 7 / 4 = 1.75 T = 7 / 4 = 1.75
T = 7 / 4 = 1.75


 -
-  T)2 n
T)2 n -
-  T)2 n
T)2 n = 1.5
= 1.5 = 2
= 2 = 1.75
= 1.75 = 1.75
= 1.75