Uno de los análisis estadísticos más comunes en la práctica es probablemente el utilizado para comparar dos grupos independientes de observaciones con respecto a una variable numérica. Como ejemplo, consideremos los datos que se muestran en la Tabla 1, correspondientes a 75 individuos con sobrepeso sometidos a dos dietas alimenticias distintas, de modo que se desea comparar el peso de los individuos que iniciaron cada una de las dietas.
Como ya se ha adelantado, la aplicación de un contraste paramétrico requiere la normalidad de las observaciones para cada uno de los grupos. La comprobación de esta hipótesis puede realizarse tanto por métodos gráficos (por medio de histogramas, diagramas de cajas o gráficos de normalidad) como mediante tests estadísticos5 (test de Kolmogorov-Smirnov, test de Shapiro-Wilks). Un número suficiente de observaciones (digamos mayor de 30) como ocurre en el ejemplo planteado justifica, no obstante, la utilización del mismo test. Así mismo, este tipo de metodología exigirá que la varianza en ambos grupos de observaciones sea la misma. En primer lugar se desarrollará el test t de Student para el caso en el que se verifiquen ambas condiciones, discutiendo posteriormente el modo de abordar formalmente el caso en el que las varianzas no sean similares.
Bajo las hipótesis de normalidad e igual varianza la comparación de ambos grupos puede realizarse en términos de un único parámetro como el valor medio (Figura 1a), de modo que en el ejemplo planteado la hipótesis de partida será, por lo tanto:
H0: La media de peso inicial es igual en ambos grupos
Se denotará por {X1, X2,...,Xn}
e {Y1,Y2,...,Ym} al peso observado en cada uno de los sujetos sometidos a la dieta A y a la
dieta B respectivamente. En general no se exigirá que coincida el número
de observaciones en cada uno de los grupos que se comparan, de modo que en
el ejemplo n=40 y m=35.El t test para dos muestras independientes se basa en el estadístico:
(1)
dondee
denotan el peso medio en cada uno de los grupos:
y,
las cuasivarianzas muestrales correspondientes:
Con lo cual, en este caso particular, el valor utilizado para el contraste será:
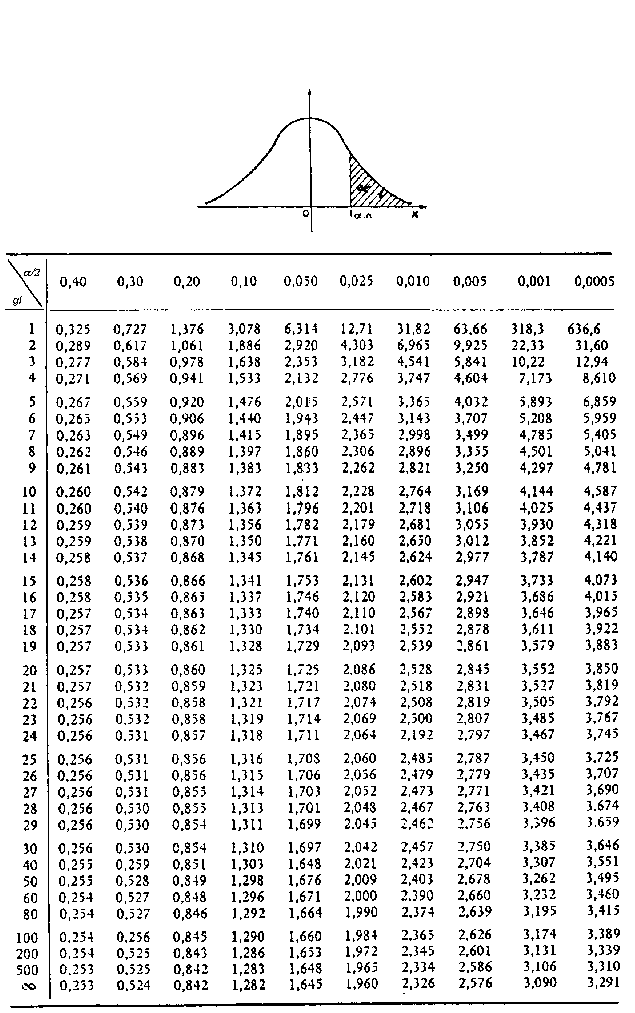
Si la hipótesis de partida es cierta el estadístico (1) seguirá una distribución t de Student con n+m-2 grados de libertad. De ser así, el valor obtenido debería estar dentro del rango de mayor probabilidad según esta distribución (Figura 2). Usualmente se toma como referencia el rango de datos en el que se concentra el 95% de la probabilidad. El valor-p que usualmente reportan la mayoría de paquetes estadísticos no es más que la probabilidad de obtener, según esa distribución, un dato más extremo que el que proporciona el test. Como ya se dijo, refleja también la probabilidad de obtener los datos observados si fuese cierta la hipótesis inicial. Si el valor-p es muy pequeño (usualmente se considera p<0.05) es poco probable que se cumpla la hipótesis de partida y se debería de rechazar. La región de aceptación corresponde por lo tanto a los valores centrales de la distribución para los que p>0.05. En el ejemplo planteado el valor-p correspondiente es de 0.425, de modo que no existe evidencia estadística de que el peso medio en ambos grupos sea diferente. En la Tabla 2, se determina los grados de libertad (en la primera columna) y el valor de α (en la primera fila). El número que determina su intersección es el valor crítico correspondiente. De este modo, si el estadístico que se obtiene toma un valor mayor se dirá que la diferencia es significativa.
Otro modo de obtener esta misma información es mediante el cálculo de intervalos de confianza para la diferencia de la respuesta media en ambos grupos. A mayores, el intervalo de confianza constituye una medida de la incertidumbre con la que se estima esa diferencia a partir de la muestra, permitiendo valorar tanto la significación estadística como la magnitud clínica de esa diferencia6. En el caso que nos ocupa, el intervalo de confianza vendrá dado como:
dondedenota el valor que según la distribución t de Student con n+m-2 grados de libertad deja a su derecha el 2.5% de los datos. En el ejemplo, el intervalo de confianza con una seguridad del 95% para la diferencia de peso viene dado por:
A medida que el tamaño muestral aumenta, la distribución del estadístico (1) se hace más próxima a la de una variable Normal estándar. De este modo, en algunos textos se opta por utilizar esta distribución para realizar la comparación de medias. Aunque esta aproximación es correcta para muestras suficientemente grandes, ambos métodos proporcionan en este caso resultados prácticamente idénticos, por lo que resulta más simple utilizar, independientemente del tamaño de la muestra, la misma metodología a partir de la distribución t. El mismo planteamiento podría utilizarse en el caso de varianzas distintas o de muestras apareadas.
Tabla 1. Datos de 75 pacientes con sobrepeso sometidos a dos dietas alimenticias.
|
|||||
| Dieta | Peso inicial | Peso final | Dieta | Peso inicial | Peso final |
A
|
94,07
|
86,59
|
B
|
88,02
|
84,12
|
A
|
96,79
|
93,08
|
B
|
88,22
|
86,13
|
A
|
92,15
|
87,85
|
B
|
103,45
|
101,21
|
A
|
92,30
|
86,83
|
B
|
82,94
|
79,08
|
A
|
96,50
|
92,70
|
B
|
89,71
|
86,19
|
A
|
83,11
|
76,80
|
B
|
94,83
|
91,93
|
A
|
91,16
|
83,40
|
B
|
81,93
|
78,97
|
A
|
90,81
|
86,74
|
B
|
83,41
|
78,89
|
A
|
81,37
|
77,67
|
B
|
73,59
|
69,76
|
A
|
89,81
|
85,70
|
B
|
108,47
|
104,20
|
A
|
84,92
|
79,96
|
B
|
72,67
|
70,01
|
A
|
84,43
|
79,80
|
B
|
96,84
|
93,66
|
A
|
86,33
|
81,15
|
B
|
88,48
|
87,00
|
A
|
87,60
|
81,92
|
B
|
89,57
|
87,24
|
A
|
81,08
|
76,32
|
B
|
85,22
|
82,09
|
A
|
92,07
|
90,20
|
B
|
103,76
|
102,24
|
A
|
81,14
|
73,34
|
B
|
87,84
|
84,66
|
A
|
96,87
|
93,58
|
B
|
91,50
|
88,95
|
A
|
99,59
|
92,36
|
B
|
93,04
|
88,73
|
A
|
83,90
|
77,23
|
B
|
92,14
|
88,07
|
A
|
89,41
|
85,45
|
B
|
85,26
|
81,36
|
A
|
85,31
|
84,59
|
B
|
89,42
|
86,64
|
A
|
89,25
|
84,89
|
B
|
92,42
|
88,99
|
A
|
93,20
|
93,10
|
B
|
93,13
|
89,73
|
A
|
89,17
|
86,87
|
B
|
80,86
|
77,81
|
A
|
93,51
|
86,36
|
B
|
88,75
|
85,93
|
A
|
88,85
|
83,24
|
B
|
95,02
|
91,90
|
A
|
88,40
|
81,20
|
B
|
92,29
|
91,28
|
A
|
82,45
|
77,18
|
B
|
89,43
|
87,22
|
A
|
96,47
|
88,61
|
B
|
93,32
|
89,77
|
A
|
99,48
|
94,67
|
B
|
92,88
|
89,38
|
A
|
99,95
|
93,87
|
B
|
89,88
|
88,00
|
A
|
100,05
|
94,15
|
B
|
82,25
|
80,81
|
A
|
87,33
|
82,17
|
B
|
88,99
|
86,87
|
A
|
87,61
|
86,01
|
B
|
82,07
|
79,74
|
A
|
89,28
|
83,78
|
|||
A
|
89,72
|
83,56
|
|||
A
|
95,57
|
89,58
|
|||
A
|
97,71
|
91,35
|
|||
A
|
98,73
|
97,82
|
|||
| Figura 1. Comparación de dos poblaciones normales |
| a) Poblaciones normales con igual varianza y medias distintas |
 |
Tabla 2. Distribución t de Student
|
 |
Dos muestras independientes con Varianza distinta
El caso en el que se dispone de dos grupos de observaciones independientes con diferentes varianzas, la distribución de los datos en cada grupo no puede compararse únicamente en términos de su valor medio (Figura 1b). El contraste estadístico planteado en el apartado anterior requiere de alguna modificación que tenga en cuenta la variabilidad de los datos en cada población. Obviamente, el primer problema a resolver es el de encontrar un método estadístico que nos permita decidir si la varianza en ambos grupos es o no la misma. El F test o test de la razón de varianzas viene a resolver este problema. Bajo la suposición de que las dos poblaciones siguen una distribución normal y tienen igual varianza se espera que la razón de varianzas:
siga una distribución F de Snedecor con parámetros (n-1) y (m-1).
Supongamos que en el ejemplo anterior se desee comparar la pérdida de peso en los sujetos sometidos a cada una de las dos dietas. La aplicación del estadístico (1) no será factible, ya que las varianzas en ambos grupos son sustancialmente distintas. En este caso la razón de varianzas es de 3.97 / 0.80 = 4.96, valor que se debe comparar con una distribución F39,34. El valor-p asociado será p<0.01, siendo muy poco probable que las observaciones provengan de poblaciones con igual variabilidad.
En este tipo de situaciones, donde no se debe aplicar el contraste basado en (1), podemos utilizar una modificación del t test para el caso de varianzas desiguales, conocido como el test de Welch7 basada en el estadístico:
que, bajo la hipótesis nula seguirá una distribución t de Student con un número f de grados de libertad que dependerá de las varianzas muestrales según la expresión:
La técnica para realizar el contraste es análoga a la vista anteriormente cuando las varianzas son desconocidas e iguales. Por ejemplo, en el caso planteado, la pérdida media de peso para los individuos en cada una de las dietas fue dee
con las variabilidades anteriormente expresadas. Esto conduce a un valor del estadístico de t=5.58 a relacionar con una distribución t de Student con aproximadamente 56 grados de libertad. El valor-p resultante es, por lo tanto, p<0.001 con lo cual podemos rechazar la hipótesis de partida y concluir que la reducción de peso experimentada es distinta según la dieta que se siga.
Al igual que en el caso anterior, podrá optarse por calcular el correspondiente 95% intervalo de confianza para la diferencia de medias dado por:
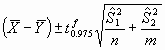
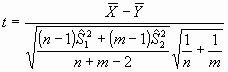
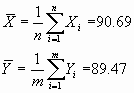
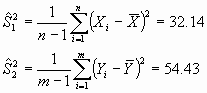
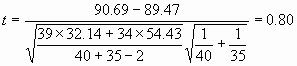
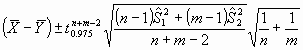
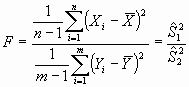
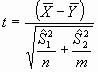
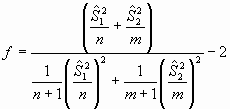
No hay comentarios:
Publicar un comentario