Estadistica Descriptiva:
Estudio de los métodos para la obtencion, organizacion, presentacion y descrpcion de informacion numérica.
Las medidas de tendencia central (media, mediana y moda) sirven como puntos de referencia para interpretar las calificaciones que se obtienen en una prueba.
La media aritmética: comúnmente conocida como media o promedio. Se representa por medio de una letra M o por una X con una línea en la parte superior.
La mediana: la cual es el puntaje que se ubica en el centro de una distribución. Se representa como Md.
La moda: que es el puntaje que se presenta con mayor frecuencia en una distribución. Se representa Mo.
De estas tres medidas de tendencia central, la media es
reconocida como la mejor y más útil. Sin embargo, cuando en una
distribución se presentan casos cuyos puntajes son muy bajos o muy
altos respecto al resto del grupo, es recomendable utilizar la mediana o
la moda. (Porque dadas las características de la media, esta es
afectada por los valores extremos).
La media es considerada como la mejor medida de tendencia central, por las siguientes razones:
Los puntajes contribuyen de manera proporcional al hacer el cómputo de la media.
Es la medida de tendencia central más conocida y utilizada.
Las medias de dos o más distribuciones pueden ser fácilmente promediadas mientras que las
medianas y las modas de las distribuciones no se promedian.
La media se utiliza en procesos y técnicas estadísticas más complejas mientras que la mediana y la
moda en muy pocos casos.
Media aritmética 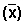 o promedio
o promedio
Es aquella medida que se obtiene al dividir la suma de todos los valores de una variable por la frecuencia total. En palabras más simples, corresponde a la suma de un conjunto de datos dividida por el número total de dichos datos.
Ejemplo 1:
En matemáticas, un alumno tiene las siguientes notas: 4, 7, 7, 2, 5, 3
n = 6 (número total de datos)
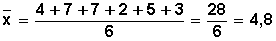
La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio.
En matemáticas, un alumno tiene las siguientes notas: 4, 7, 7, 2, 5, 3
n = 6 (número total de datos)
La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio.
Moda (Mo)
Es la medida que indica cual dato tiene la mayor frecuencia en un conjunto de datos; o sea, cual se repite más.Ejemplo 1:
Determinar la moda en el siguiente conjunto de datos que corresponden a las edades de niñas de un Jardín Infantil.
5, 7, 3, 3, 7, 8, 3, 5, 9, 5, 3, 4, 3
La edad que más se repite es 3, por lo tanto, la Moda es 3 (Mo = 3)
Mediana (Med)
Para reconocer la mediana, es necesario tener ordenados los valores sea de mayor a menor o lo contrario. Usted divide el total de casos (N) entre dos, y el valor resultante corresponde al número del caso que representa la mediana de la distribución.Es el valor central de un conjunto de valores ordenados en forma creciente o decreciente. Dicho en otras palabras, la Mediana corresponde al valor que deja igual número de valores antes y después de él en un conjunto de datos agrupados.
Según el número de valores que se tengan se pueden presentar dos casos:
Si el número de valores es impar, la Mediana corresponderá al valor central de dicho conjunto de datos.
Si el número de valores es par, la Mediana corresponderá al promedio de los dos valores centrales (los valores centrales se suman y se dividen por 2).
Ejemplo 1:
Se tienen los siguientes datos: 5, 4, 8, 10, 9, 1, 2
Al ordenarlos en forma creciente, es decir de menor a mayor, se tiene: 1, 2, 4, 5, 8, 9, 10
El 5 corresponde a la Med, porque es el valor central en este conjunto de datos impares.
Construccion de tablas de distribucion.
Las medidas de dispersión nos informan sobre cuánto se alejan del centro los valores de la distribución.
Desviacion media:
Es la sumaa de los valores absolutos de las desviaciones de los datos con respecto a la media (valor fijo) divididos por el tamaño de la muestra.
Es la sumaa de los valores absolutos de las desviaciones de los datos con respecto a la media (valor fijo) divididos por el tamaño de la muestra.
Varianza:
Se representa asi: S2. Mide la variabilidad de los datos con respecto a la media, en unidades cuadradas.
Una caracteristica de la varianza es que, al elevar al cuadrado las disviaciones grandes, las aumenta considerablemente, mientras que hace dismnuir las variaciones pequeñas, 10 al cuadrado = 100, aumenta; 0.1 al cuarado = 0.01, disminuye.
Desviacion estandar:
Se reresenta asi: S si se esta trabajando on una muestra y asi: σ si se trabaja con una poblacion.
Es laa raiz cuadrada de la varianza.
Se reresenta asi: S si se esta trabajando on una muestra y asi: σ si se trabaja con una poblacion.
Es laa raiz cuadrada de la varianza.
No hay comentarios:
Publicar un comentario